Briefly, a cellular automaton consist of a lattice of discrete identical sites, each site taking on a finite set of values. The values of the sites evolve in discrete time steps according to a set of rules that specify the value of each site in terms of the values of neighboring sites. The main components of a CA are:
-- the grid
-- the neighboors
-- the set of rules
-- the initial conditions.
In our examples we use a rectangular grid and two type of neighboor vonNewman (a) and Moore (b), see figure
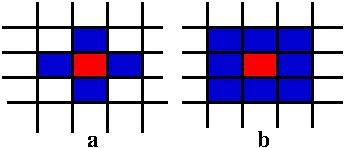
Here we illustrate a number of 3 discrete systems: forest fire, sand piles, and game of life.
Bibliography:
Stephen Wolfram, A New Kind of Science, Wolfram Media, Inc., 2002.
Jane Molofsky and James D. Bever, A New Kind of Ecology?, BioScience, 54(5), 2004.
The forest fire model is a probabilistc cellular automaton defined on d-dimensional lattice, in our exemaple a 2D square.
Each site can be in one of three states: empty, green tree or burning tree.
The update rules:
(a) an empty site become a green tree with a p probability,
(b) a burning site become an emty site and
(c) a green tree become a burning tree if at least one of its neighbors is a burning tree.
Runnig examples:
p=0.03;0.04;0.05;0.08
Bibliography:
P. Bak, K. Chen, and C. Tang, A forest fire model and some thoughts on turbulence, Phys. Lett. A. 147(5,6), (1990)
B. Drossel and F. Schwabl, Self Organized Critical Forest-Fire Model, Phys. Rev. Lett. 69(11), (1992)
Each site can be in one of three states: empty, green tree or burning tree.
The update rules:
(a) an empty site become a green tree with a p probability,
(b) a burning site become an emty site and
(c) a green tree become a burning tree if at least one of its neighbors is a burning tree.
Runnig examples:
p=0.03;0.04;0.05;0.08
Bibliography:
P. Bak, K. Chen, and C. Tang, A forest fire model and some thoughts on turbulence, Phys. Lett. A. 147(5,6), (1990)
B. Drossel and F. Schwabl, Self Organized Critical Forest-Fire Model, Phys. Rev. Lett. 69(11), (1992)
Sand pile models is an example of dynamical system with extend spatial degrees of freedom.
This kind of systems evolve into self-organized critical state [Bak].
The rules of evolution:
vonNewmann $$ \begin{array}{rl} z(x,y)\rightarrow&z(x,y)-4\\ z(x\pm 1,y)\rightarrow&z(x\pm 1,y)+1\\ z(x,y\pm 1)\rightarrow&z(x,y\pm 1)+1\\ &{\rm for\,\,} z(x,y)\leq 5 \end{array} $$ Moore $$ \begin{array}{rl} z(x,y)\rightarrow&z(x,y)-8\\ z(x\pm 1,y)\rightarrow&z(x\pm 1,y)+1\\ z(x,y\pm 1)\rightarrow&z(x,y\pm 1)+1\\ z(x\pm 1,y\pm 1)\rightarrow&z(x\pm ,y\pm 1)+1\\ &{\rm for\,\,} z(x,y)\leq 9 \end{array} $$ Running examples:
Source grain numbers= 100, 30 000, 60 000;
Bibliography:
P. Bak, C. Tang and K. Wiesefeld Self organized criticality, Phys. Lett. A. 38(1), (1988)
Deepak Dhar, Theoretical studies of self-organized criticality, Physica A, 369, pp. 29-70, 2006.
The rules of evolution:
vonNewmann $$ \begin{array}{rl} z(x,y)\rightarrow&z(x,y)-4\\ z(x\pm 1,y)\rightarrow&z(x\pm 1,y)+1\\ z(x,y\pm 1)\rightarrow&z(x,y\pm 1)+1\\ &{\rm for\,\,} z(x,y)\leq 5 \end{array} $$ Moore $$ \begin{array}{rl} z(x,y)\rightarrow&z(x,y)-8\\ z(x\pm 1,y)\rightarrow&z(x\pm 1,y)+1\\ z(x,y\pm 1)\rightarrow&z(x,y\pm 1)+1\\ z(x\pm 1,y\pm 1)\rightarrow&z(x\pm ,y\pm 1)+1\\ &{\rm for\,\,} z(x,y)\leq 9 \end{array} $$ Running examples:
Source grain numbers= 100, 30 000, 60 000;
Bibliography:
P. Bak, C. Tang and K. Wiesefeld Self organized criticality, Phys. Lett. A. 38(1), (1988)
Deepak Dhar, Theoretical studies of self-organized criticality, Physica A, 369, pp. 29-70, 2006.
A cell can be in two states: alive cell or dead cell.
The rule of evolution:
Dead cell: Become an alive cell if it has exactly 3 alive neigbors, otherwise reamin dead
Alive cell: Become a dead cell if it has more of 4 alive cell or less than 1 alive cell, otherwise remain alive.
Runnig examples:
Bibliography:
Conway's Game of Life - Stanford University
The rule of evolution:
Dead cell: Become an alive cell if it has exactly 3 alive neigbors, otherwise reamin dead
Alive cell: Become a dead cell if it has more of 4 alive cell or less than 1 alive cell, otherwise remain alive.
Runnig examples:

Bibliography:
Conway's Game of Life - Stanford University
Rule of random walk.